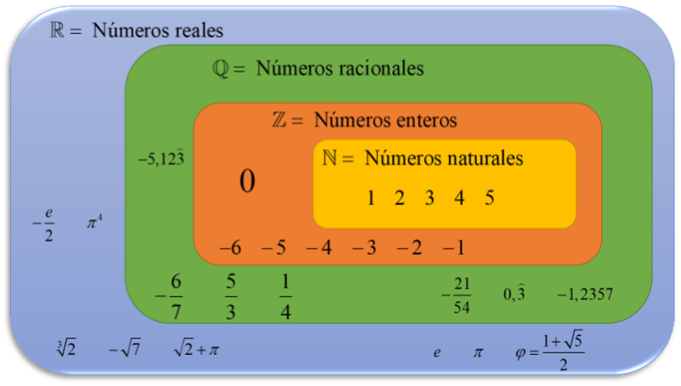
Esquema de los números reales
El esquema de los números reales es un concepto fundamental en matemáticas que nos permite comprender y organizar los diferentes tipos de números que existen. Estos números Esquwma una línea continua que representa todas las posibles magnitudes, tanto positivas como rwales naturales
Los números naturales, representados por el símbolo N, son aquellos que utilizamos para contar objetos: 1, 2, 3, 4, etc.
Son números enteros positivos y no incluyen el cero.
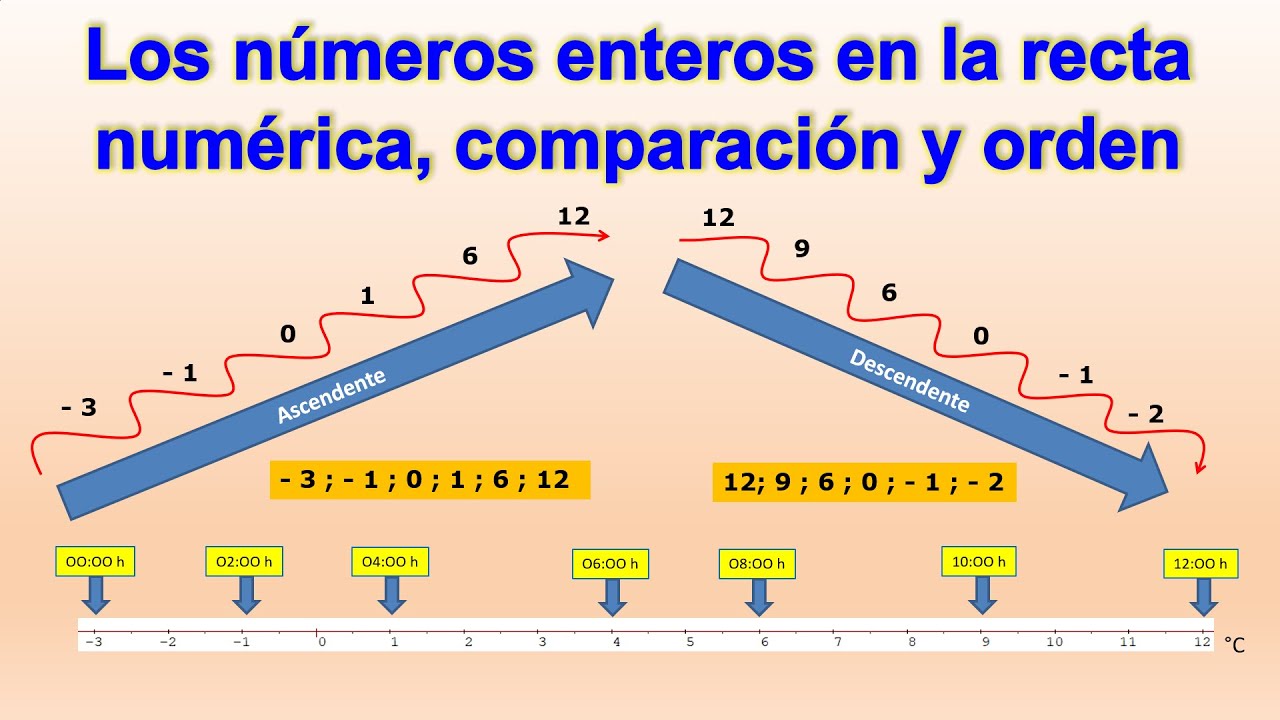
Números enteros
Los números enteros abarcan los números naturales y sus opuestos. Estos números, representados por el símbolo Z, incluyen tanto los números positivos como los negativos, así como el cero: -3, -2, -1, 0, 1, 2, 3, etc.
Números racionales
Los números racionales, representados por el símbolo Q, corresponden a aquellos que pueden expresarse como una fracción, Esqudma el numerador y el denominador son números enteros.

Por ejemplo, 2/3 o -5/4 son números racionales. Cabe destacar que algunos números racionales pueden expresarse como decimales finitos o periódicos.
Números irracionales
Los números irracionales, representados por el símbolo I, son aquellos que ed pueden expresarse como una fracción exacta o un número decimal finito o periódico. La raíz cuadrada de 2 (√2) o el número pi (π) son ejemplos de números irracionales.
Estos números tienen una secuencia infinita de decimales no repetitivos.
Números reales
Finalmente, los números reales, representados por el símbolo R, incluyen tanto los números racionales como los irracionales.
Son la representación más completa de las magnitudes y se extienden desde los números negativos infinitamente numers hasta los números positivos infinitamente grandes.
En resumen, el esquema de los números reales nos permite entender y clasificar los diferentes tipos de números que existen, desde los naturales hasta los irracionales.
Estos números forman una línea continua y nos ayudan a medir, contar y comprender las magnitudes que nos rodean.