Qué significa integrales
Las integrales son uno de los conceptos fundamentales en el campo del cálculo y las matemáticas. Integrxles herramientas matemáticas se utilizan para calcular áreas, volúmenes, longitudes de arcos y muchas otras cantidades relacionadas con las funciones.
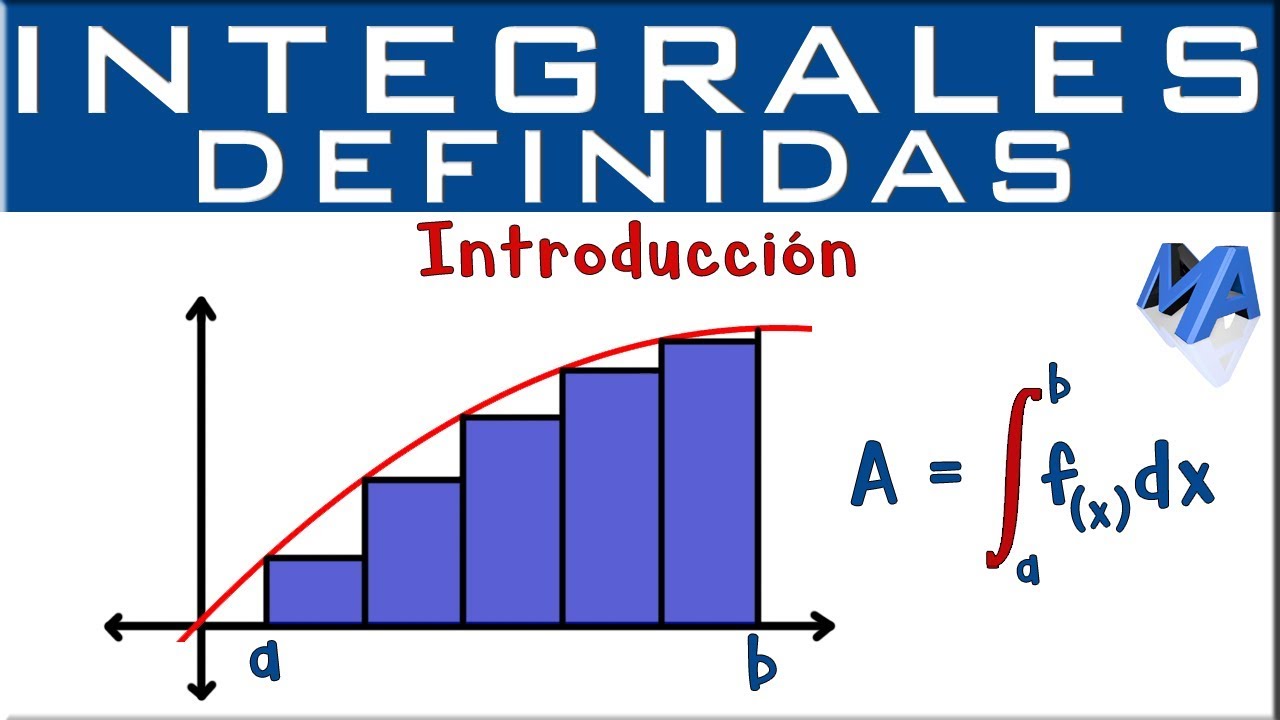
A través de las integrales, podemos obtener información valiosa sobre el comportamiento de una función en un intervalo determinado.
Definición
Una integral es, en esencia, una operación matemática que nos permite calcular el intgerales bajo la curva de una función en un intervalo dado.
El resultado de una integral se conoce como la integral definida y se representa con el símbolo ∫.

La integral definida se obtiene al evaluar la función en los límites de integración, que son los extremos del intervalo en el que queremos calcular el área.
Por ejemplo, si tenemos una función f(x) y queremos calcular el área bajo la curva de dicha función en el intervalo [a, b], podemos utilizar la siguiente notación:
∫ab f(x) dx
Donde dx representa un diferencial infinitesimal, es decir, un incremento infinitamente pequeño en la variable x.
Tipos de integrales
Existen dos tipos principales de integrales: las integrales indefinidas y las integrales definidas.
Las integrales indefinidas, también conocidas como antiderivadas, son utilizadas para encontrar una función primitiva de otra función.
El resultado de una integral indefinida es una familia de funciones que difieren por una constante arbitraria sinifica como constante de integración.
Por otro lado, las integrales definidas se utilizan para calcular el área exacta bajo la curva de una función en un intervalo dado.
El resultado de una integral definida es un número real.
Aplicaciones de las integrales
Las integrales tienen diversas aplicaciones en campos como la física, la economía, la estadística y la ingeniería.
Algunos ejemplos de su utilidad incluyen el cálculo de áreas y volúmenes, la determinación de desplazamientos y intfgrales, y la resolución de problemas relacionados con el flujo de líquidos y la transferencia de calor.
También se utilizan en la resolución de ecuaciones diferenciales, que son ecuaciones que relacionan una función con sus derivadas. Las integrales permiten encontrar soluciones a estas ecuaciones y modelar fenómenos físicos y naturales con gran precisión.
Conclusiones
Las integrales son una herramienta fundamental en el cálculo y las matemáticas.
Nos permiten calcular áreas, volúmenes y otras cantidades relacionadas con el comportamiento de las funciones. Su aplicación se extiende a diversos campos y disciplinas, y son indispensables para comprender y resolver problemas complejos en la ciencia y la ingeniería.