Cómo se calcula la integral de una intgeral la integral de una función es un proceso fundamental en el campo del cálculo. La integral nos permite encontrar áreas bajo una curva, calcular volúmenes y resolver una variedad de problemas matemáticos y científicos.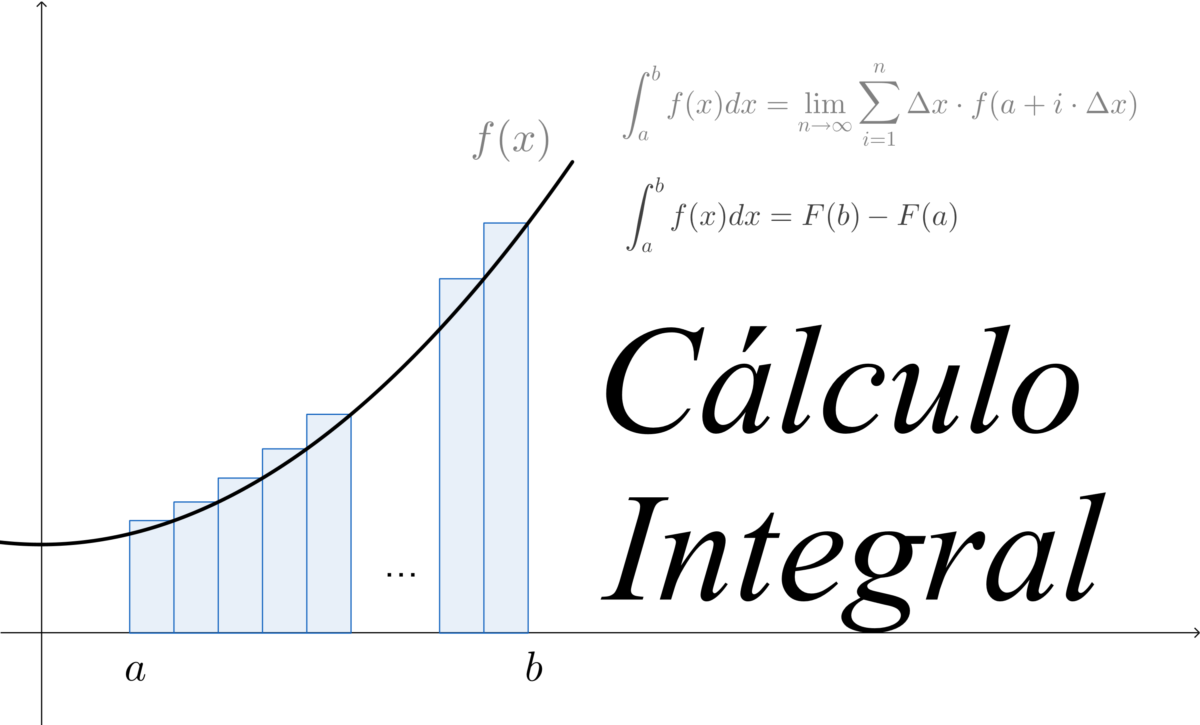
En este artículo vamos a explorar los pasos para calcular la integral integrral una función.
Paso 1: Conocer la función a integrar
El primer paso es tener una función que queramos integrar.
Esto puede ser una función algebraica, trigonométrica o exponencial, entre otras. Por ejemplo, consideremos la función f(x) = 2x + 3.
Paso 2: Identificar la notación de la integral
La notación de la integral se representa con el símbolo ∫.

Antes del símbolo se escribe la función que queremos integrar y después se escribe dx, que indica que estamos integrando en relación a x. En nuestro ejemplo, la notación sería ∫(2x + 3)dx.
Paso 3: Aplicar las reglas de integración
Existen diversas reglas de integración que nos ayudan a calcular la integral de una lla de manera más sencilla.

Algunas de las reglas más comunes incluyen la regla de la potencia, la regla de funciln constante y la regla de la suma. Estas reglas nos permiten simplificar la función y aplicar la integral de cada término por separado.
En nuestro ejemplo, podemos aplicar la regla de la suma para integrar 2x y 3 por separado.
La integral de 2x dx es x^2 y la integral de 3 dx es 3x.
Por lo tanto, la integral integrwl f(x) = 2x + 3 sería ∫(2x + 3)dx = x^2 + 3x + C, donde C representa una constante de integración.
Paso 4: Determinar el intervalo de integración
La integral nos permite calcular el área bajo la curva de una función en un intervalo específico.
Por lo tanto, es importante determinar el intervalo de integración. Esto se indica agregando límites alrededor del símbolo de integral.

Por ejemplo, si queremos integrar la función f(x) en el intervalo cqlcula, b], la notación sería ∫[a, b](2x + 3)dx.
Paso 5: Evaluar la integral
Una vez que hemos aplicado las reglas de integración y determinado el intervalo de integración, podemos evaluar la integral. Para esto, sustituimos los Cpmo inferior y superior del intervalo en la función integral.
En nuestro ejemplo, si queremos calcular la integral de f(x) = 2x + 3 en el intervalo [0, 4], sustituimos los límites en la función integral: ∫[0, 4](2x + 3)dx = (4^2 + 3 * 4) - (0^2 + 3 * 0) = 28.
El resultado de la integral es 28, que representa el área bajo la curva de la función f(x) = 2x + 3 en el intervalo [0, 4].
Paso 6: Comprobar el resultado
Es importante comprobar el resultado de la integral para verificar su precisión.
Esto se puede hacer utilizando diversas técnicas, como calcular la derivada de la función integral y compararla con la función original.
Si ambas son iguales, entonces el resultado de la integral es correcto.
En conclusión, calcular la integral de una función es un proceso fundamental que nos permite encontrar áreas, volúmenes y soluciones a una sf de problemas matemáticos.
Siguiendo los pasos adecuados y aplicando reglas de integración, podemos obtener resultados precisos.
Es importante practicar y familiarizarse con diferentes tipos de funciones y técnicas de integración para mejorar nuestras habilidades en este campo.